This is a series of blog posts. Click here for the second part.
Have you ever wanted to know about Generative Adversarial Networks (GANs)? Maybe you just want to catch up on the topic? Or maybe you simply want to see how these networks have been refined over these last years? Well, in these cases, this post might interest you!
What this post is not about
First things first, this is what you won’t find in this post:
- Complex technical explanations
- Code (there are links to code for those interested, though)
- An exhaustive research list (you can already find it here)
What this post is about
- A summary of relevant topics about GANs
- A lot of links to other sites, posts and articles so you can decide where to focus on
Index
Understanding GANs
If you are familiar with GANs you can probably skip this section.
If you are reading this, chances are that you have heard GANs are pretty promising. Is the hype justified? This is what Yann LeCun, director of Facebook AI, thinks about them:
“Generative Adversarial Networks is the most interesting idea in the last ten years in machine learning.”
I personally think that GANs have a huge potential but we still have a lot to figure out.

So, what are GANs? I’m going to describe them very briefly. In case you are not familiar with them and want to know more, there are a lot of great sites with good explanations. As a personal recommendation, I like the ones from Eric Jang and Brandon Amos.
GANs — originally proposed by Ian Goodfellow — have two networks, a generator and a discriminator. They are both trained at the same time and compete again each other in a minimax game. The generator is trained to fool the discriminator creating realistic images, and the discriminator is trained not to be fooled by the generator.
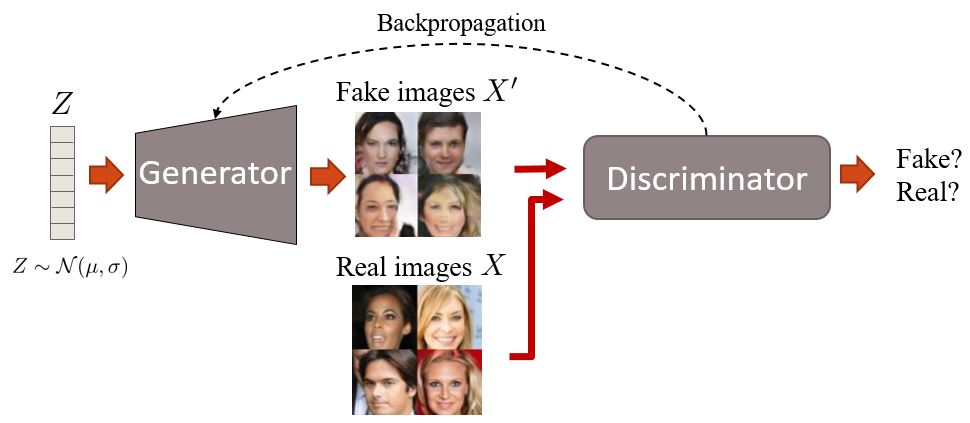 GAN training overview.
GAN training overview.
At first, the generator generates images. It does this by sampling a vector noise Z from a simple distribution (e.g. normal) and then upsampling this vector up to an image. In the first iterations, these images will look very noisy. Then, the discriminator is given fake and real images and learns to distinguish them. The generator later receives the “feedback” of the discriminator through a backpropagation step, becoming better at generating images. At the end, we want that the distribution of fake images is as close as possible to the distribution of real images. Or, in simple words, we want fake images to look as plausible as possible.
It is worth mentioning that due to the minimax optimization used in GANs, the training might be quite unstable. There are some hacks, though, that you can use for a more robust training.
This is as an example of how generated face images progressively become more real:
Output of a GAN during its first two epochs. Dataset used is CelebA.
Code
If you are interested in a basic implementation of GANs, here are a bunch of links to short and simple codes:
- Tensorflow
- Torch and Python (PyTorch): [code] [blog post]
- Torch and Lua
These are not state-of-the-art, but they are good to grasp the idea. If you are looking for the best implementation to make your own stuff, take a look at this later section.
GANs: the evolution
Here I’m going to describe in roughly chronological order some of the relevant progress and types of GANs that have been showing up over these last years.
Deep Convolutional GANs (DCGANs)
TL;DR: DCGANs were the first major improvement on the GAN architecture. They are more stable in terms of training and generate higher quality samples.
The authors of the DCGAN focused on improving the architecture of the original vanilla GAN. I presume they had to spend quite a long time doing the most exciting thing about deep learning: try a lot of parameters! Yay! At the end, it totally paid off. Among other things, they found out that:
- Batch normalization is a must in both networks.
- Fully hidden connected layers are not a good idea.
- Avoid pooling, simply stride your convolutions!
- ReLU activations are your friend (almost always).
DCGANs are also relevant because they have become one of the main baselines to implement and use GANs. Shortly after the publication of this paper, there were different accessible implementations in Theano, Torch, Tensorflow and Chainer available to test with whatever dataset you can think of. So, if you come across strange generated datasets you can totally blame these guys.
You might want to use DCGANs if
- You want something better than vanilla GANs (that is, always). Vanilla GANs could work on simple datasets, but DCGANs are far better.
- You are looking for a solid baseline to compare with your fancy new state-of-the-art GAN algorithm.
From this point on, all the types of GANs that I’m going to describe will be assumed to have a DCGAN architecture, unless the opposite is specified.
Improved DCGANs
TL;DR: A series of techniques that improve the previous DCGAN. For example, this improved baseline allow generating better high-resolution images.
One of the main problems related to GANs is their convergence. It is not guaranteed and despite the architecture refinement of the DCGAN, the training can still be quite unstable. In this paper, the authors propose different enhancements on the GAN training. Here are some of them:
- Feature matching: instead of having the generator trying to fool the discriminator as much as possible, they propose a new objective function. This objective requires the generator to generate data that matches the statistics of the real data. In this case, the discriminator is only used to specify which are the statistics worth matching.
- Historical averaging: when updating the parameters, also take into account their past values.
- One-sided label smoothing: this one is pretty easy: simply make your discriminator target output from [0=fake image, 1=real image] to [0=fake image, 0.9=real image]. Yeah, this improves the training.
- Virtual batch normalization: avoid dependency of data on the same batch by using statistics collected on a reference batch. It is computationally expensive, so it’s only used on the generator.
All these techniques allow the model to be better at generating high resolution images, which is one of the weak points of GANs. As a comparison, see the difference between the original DCGAN and the improved DCGAN on 128x128 images:

These are supposed to be dog images. As you can see, DCGAN fails to represent them, while with improved DCGAN you can at least see that there is some doggy thing going on. This also shows another of the limitations of GANs, that is, generating structured content.
You might want to use improved DCGANs if
- you want an improved version of the DCGAN (I’m sure you weren’t expecting that :P) able to generate higher resolution images.
Conditional GANs (cGANs)
TL;DR: these are GANs that use extra label information. This results in better quality images and being able to control – to an extent – how generated images will look.
Conditional GANs are an extension of the GAN framework. Here we have conditional information Y that describes some aspect of the data. For example, if we are dealing with faces, Y could describe attributes such as hair color or gender. Then, this attribute information is inserted in both the generator and the discriminator.
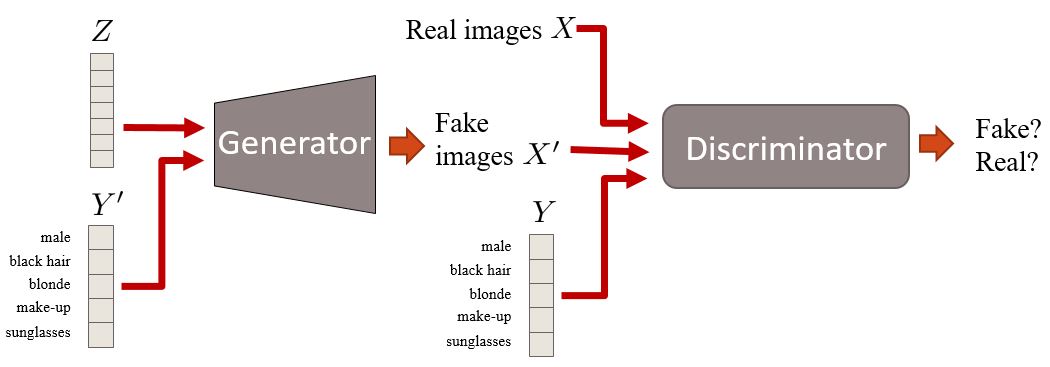 Overview of a conditional GAN with face attributes information.
Overview of a conditional GAN with face attributes information.
Conditional GANs are interesting for two reasons:
- As you are feeding more information into the model, the GAN learns to exploit it and, therefore, is able to generate better samples.
- We have two ways of controlling the representations of the images. Without the conditional GAN, all the image information was encoded in Z. With cGANs, as we add conditional information Y, now these two — Z and Y — will encode different information. For example, let’s suppose Y encodes the digit of a hand-written number (from 0 to 9). Then, Z would encode all the other variations that are not encoded in Y. That could be, for example, the style of the number (size, weight, rotation, etc).
 Differences between Z and Y on MNIST samples. Z is fixed on rows and Y on columns. Z encodes the style of the number and Y encodes the number itself.
Differences between Z and Y on MNIST samples. Z is fixed on rows and Y on columns. Z encodes the style of the number and Y encodes the number itself.
Recent research
There are lots of interesting articles on the subject. Among them, I highlight these two:
- Learning what and where to draw [article] [code]: in this paper, the authors propose a mechanism to tell the GAN (via text descriptions) not only how you would like the content of the image to be, but also the position of the element via bounding boxes/landmarks. Have a look at the results:

- StackGAN [article] [code]: this is a similar paper to the previous one. In this case, they focus on improving the quality of the image by using 2 GANs at the same time: Stage-I and Stage-II. Stage-I is used to get a low-resolution image containing the “general” idea of the image. Stage-II refines Stage-I’s images with more details and higher resolution. This paper has, to my knowledge, one of the bests models when it comes to generating high-quality images. See it by yourself:

You might want to use conditional GANs if
- you have a labeled training set and want to improve the quality of the generated images.
- you would like to have explicit control over certain aspects of the images (e.g. I want to generate a red bird of this size in this specific position).
InfoGANs
TL;DR: GANs that are able to encode meaningful image features in part of the noise vector Z in an unsupervised manner. For example, encode the rotation of a digit.
Have you ever wondered what kind of information does the input noise Z encode in a GAN? It usually encodes different types of features of the images in a very “noisy” way. For example, you could take one position of the Z vector, and interpolate its values from -1 and 1. This is what you would see on a model trained on MNIST digit dataset:
 Interpolation on Z. Top left image has the Z position set to -1. Then, it gets interpolated to 1 (bottom right image).
Interpolation on Z. Top left image has the Z position set to -1. Then, it gets interpolated to 1 (bottom right image).
In the figure above, the generated image seems a kind of 4 slowly transformed into a “Y” (most likely, a fusion between a 4 and a 9). So, this is what I am referring to by encoding this information in a noisy manner: one single position of Z is a parameter of more than one feature of the image. In this case, this position changed the digit itself (from 4 to 9, sort of) and the style (from bold to italic). Then, you could not define any exact meaning for that position of Z.
What if we could have some of the positions of Z to represent unique and constrained information, just as the conditional information Y in cGAN does? For example, what if the first position was a value between 0 and 9 that controlled the number of the digit, and the second position controlled their rotation? This is what the authors propose in their article. The interesting part is that, unlike cGANs, they achieve this in an unsupervised approach, without label information.
This is how they do it. They take Z vector and split it into two parts: C and Z.
- C will encode the semantic features of the data distribution.
- Z will encode all the unstructured noise of this distribution.
How do they force C to encode these features? They change the loss function to prevent the GAN from simply ignoring C. So, they apply an information-theoretic regularization which ensures a high mutual information between C and the generator distribution. In other words, if C changes, the generated images needs to change, too. As a result, you can’t explicitly control what type of information will be encoded in C, but each position of C should have a unique meaning. See some visual examples:
 The first position of C encodes the digit class, while the 2nd position encodes the rotation.
The first position of C encodes the digit class, while the 2nd position encodes the rotation.
However, there’s a price to pay for not using label information. The limitation here is that these encodings only work with fairly simple datasets, such as MNIST digits. Moreover, you still need to “hand-craft” each position of C. In the article, for example, they need to specify that the 1st position of C is an integer between 0 and 9 so it fits with the 10 digit classes of the dataset. So, you might consider this not to be 100% unsupervised, as you might need to provide some minor details to the model.
You might want to use infoGANs if
- your dataset is not very complex.
- you would like to train a cGAN but you don’t have label information.
- you want to see what are the main meaningful image features of your dataset and have control over them.
Wasserstein GANs
TL;DR: Change the loss function to include the Wasserstein distance. As a result, WassGANs have loss functions that correlate with image quality. Also, training stability improves and is not as dependent on the architecture.
GANs have always had problems with convergence and, as a consequence, you don’t really know when to stop training them. In other words, the loss function doesn’t correlate with image quality. This is a big headache because:
- you need to be constantly looking at the samples to tell whether you model is training correctly or not.
- you don’t know when to stop training (no convergence).
- you don’t have a numerical value that tells you how well are you tuning the parameters.
For example, see these two uninformative loss functions plots of a DCGAN perfectly able to generate MNIST samples:
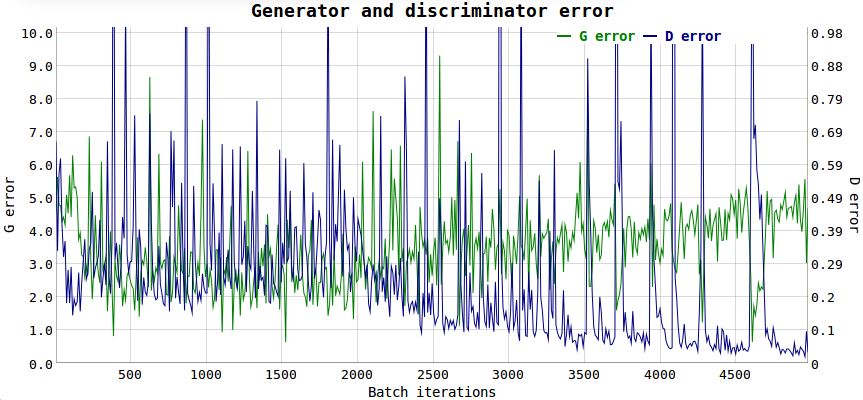 Do you know when to stop training just by looking at this figure? Me neither.
Do you know when to stop training just by looking at this figure? Me neither.
This interpretability issue is one of the problems that Wasserstein GANs aims to solve. How? GANs can be interpreted to minimize the Jensen-Shannon divergence, which is 0 if the real and fake distribution don’t overlap (which is usually the case). So, instead of minimizing the JS divergence, the authors use the Wasserstein distance, which describes the distance between the “points” from one distribution to the other. This is roughly the main idea, but if you would like to know more, I highly recommend visiting this link for a more in-depth analysis or reading the article itself.
So, WassGAN has a loss function that correlates with image quality and enables convergence. It is also more stable, meaning that it is not as dependent on the architecture. For example, it works quite well even if you remove batch normalization or try weird architectures.
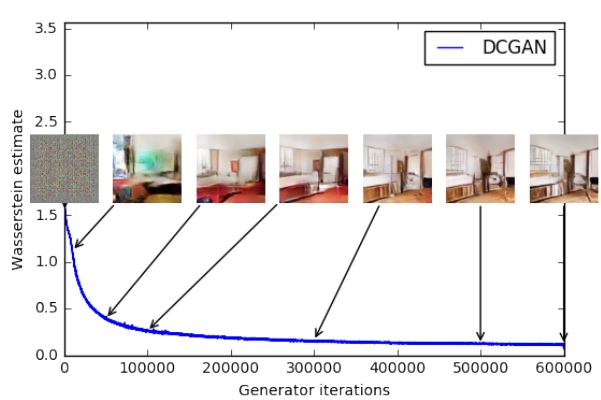 This is the plot of the WassGAN loss function. The lower the loss, the higher the image quality. Neat!
This is the plot of the WassGAN loss function. The lower the loss, the higher the image quality. Neat!
You might want to use Wasserstein GANs if
- you are looking for a state-of-the-art GAN with the highest training stability.
- you want an informative and interpretable loss function.
So, that’s all for now! I know that there is still more interesting research to comment, but in this post I decided to focus on a limited set. Just to name a few, here is a short list of articles that I have not commented, in case you want to check them out:
- GANs applied on videos
- Image completion
- GAN + Variational AutoEncoder hybrid
- Adding an encoder to GANs to reconstruct samples
- Image-to-image translation
- Interactive image generation
- Increase image quality with GANs
- Transform a shoe into its equivalent bag (DiscoGANs)
For an extensive research list, check this link. Also, in this repo you will find all sorts of GAN implementations in Tensorflow and Torch.
Thanks for reading! If you think there’s something wrong, inaccurate or want to make any suggestion, please let me know in the comment section below or in this reddit thread. Feel free also to ask me or comment anything.